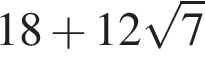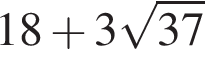Задание № 320 
i
Решение. 
Построим сечение плоскостью. Проведем прямую PN, она пересечет ребро BS в точке K. Далее проведем KM. В плоскости ABC проведем прямую, параллельную KM через точку N. Она пересечет ребро AC в точке R. Проведем MR. Трапеция NKMR — искомое сечение. Найдем ее стороны.
По теореме Менелая для треугольника 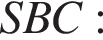
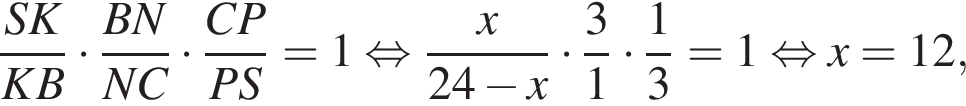

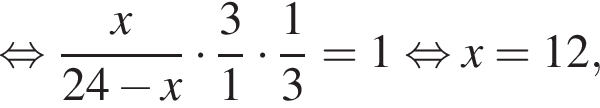
то есть точка K — середина BS. Тогда получаем, что KM параллельно BA и равно 12, как средняя линия треугольника ASB. Более того, NR так же параллельно BA и равно 6 по теореме о пропорциональных отрезках. Таким образом, трапеция NKMR — равнобедренная, найдем ее боковую сторону по теореме косинусов:
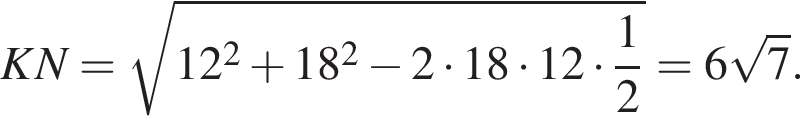
Найдем высоту трапеции по теореме Пифагора:
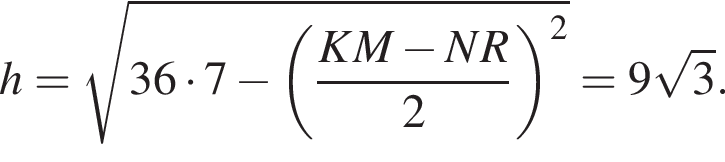
Тогда площадь трапеции равна

Ответ: 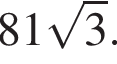
Ответ: 4
В тетраэдре SABC с ребром 24 точка P принадлежит SC так, что
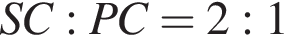 и
и 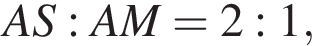
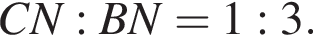 Найдите площадь сечения тетраэдра плоскостью MNP.
Найдите площадь сечения тетраэдра плоскостью MNP.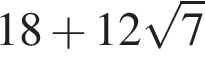
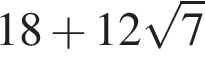


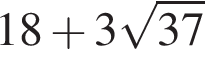
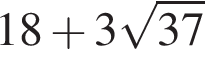
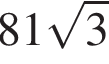
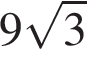
В тетраэдре SABC с ребром 24 точка P принадлежит SC так, что
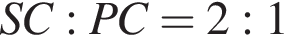 и
и 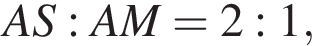
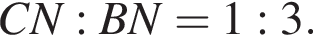 Найдите площадь сечения тетраэдра плоскостью MNP.
Найдите площадь сечения тетраэдра плоскостью MNP.